D^3CTF2019 Ancient Game V2, Thoughts & Solutions
Intro
I designed the RE challenge Ancient Game V2 in D^3CTF2019. This post talks about some designs behind this challenge along with its solution.
Challenge
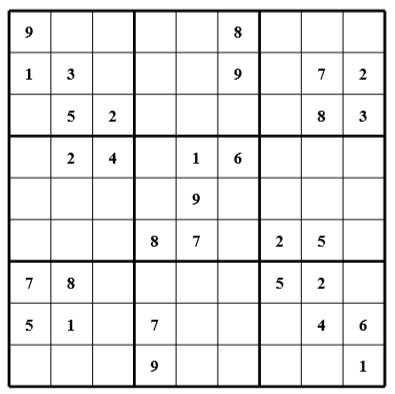
The challenge uses a virtual architecture similar to OISC to implement a classic Sudoku verification algorithm. There are four types of instructions: input, output, jcc, and NAND. As a whole, they can be seen as a NAND OISC with two I/O interrupts.
All logical operations such as XOR, AND, and OR are implemented through combinations of NAND gates. For example:
xor x,y =>
xor_tmp[0] = y NAND y
xor_tmp[1] = x NAND xor_tmp[0]
xor_tmp[2] = x NAND x
xor_tmp[3] = y NAND xor_tmp[2]
x = xor_tmp[1] NAND xor_tmp[3]
This is based on the fact that:
Q = A XOR B = [ B NAND ( A NAND A ) ] NAND [ A NAND ( B NAND B ) ]
The following is an excerpt of the Sudoku verification algorithm written in a custom DSL:
welcome = mkstr("**************************\n** Welcome To D^3CTF **\n** Ancient Game V2 **\n**************************\n\nInput Flag:")
wrong = mkstr("\nSorry, please try again.\n")
correct = mkstr("\nCorrect.\n")
flag = new(50)
// distract = new(1000)
grid = new(81)
// initialize the puzzle
set(grid[0],9)
set(grid[5],8)
set(grid[9],1)
set(grid[10],3)
set(grid[14],9)
set(grid[16],7)
...
set(grid[71],6)
set(grid[75],9)
set(grid[80],1)
__code_start__
// print the welcome message
print(welcome)
// get input
input(flag[0])
input(flag[1])
input(flag[2])
input(flag[3])
input(flag[4])
input(flag[5])
...
input(flag[46])
input(flag[47])
input(flag[48])
input(flag[49])
// transfer chars in the flag into the grids
long_transfer(flag[0],grid[1])
long_transfer(flag[1],grid[2])
...
long_transfer(flag[47],grid[77])
long_transfer(flag[48],grid[78])
long_transfer(flag[49],grid[79])
// xor with xor_table, which is introduced
// for generating different flags to different teams
grid[1] = grid[1] ^ xor_table[0]
grid[2] = grid[2] ^ xor_table[1]
grid[3] = grid[3] ^ xor_table[2]
grid[4] = grid[4] ^ xor_table[3]
grid[6] = grid[6] ^ xor_table[4]
grid[7] = grid[7] ^ xor_table[5]
...
grid[77] = grid[77] ^ xor_table[47]
grid[78] = grid[78] ^ xor_table[48]
grid[79] = grid[79] ^ xor_table[49]
// verify the sudoku game
// rows
jmp _label_wrong if grid[4] == grid[5]
jmp _label_wrong if grid[4] == grid[6]
jmp _label_wrong if grid[4] == grid[7]
...
jmp _label_wrong if grid[3] == grid[7]
jmp _label_wrong if grid[3] == grid[8]
// columns
jmp _label_wrong if grid[0] == grid[9]
jmp _label_wrong if grid[0] == grid[18]
jmp _label_wrong if grid[0] == grid[27]
...
jmp _label_wrong if grid[62] == grid[80]
jmp _label_wrong if grid[71] == grid[80]
// subgrids
jmp _label_wrong if grid[0] == grid[1]
jmp _label_wrong if grid[0] == grid[2]
jmp _label_wrong if grid[0] == grid[9]
jmp _label_wrong if grid[0] == grid[10]
...
jmp _label_wrong if grid[78] == grid[79]
jmp _label_wrong if grid[78] == grid[80]
jmp _label_wrong if grid[79] == grid[80]
// check range
jmp _label_wrong if outofnumbers(grid[1])
jmp _label_wrong if outofnumbers(grid[2])
jmp _label_wrong if outofnumbers(grid[3])
jmp _label_wrong if outofnumbers(grid[4])
...
jmp _label_wrong if outofnumbers(grid[76])
jmp _label_wrong if outofnumbers(grid[77])
jmp _label_wrong if outofnumbers(grid[78])
jmp _label_wrong if outofnumbers(grid[79])
_label_correct:
print(correct)
return
_label_wrong:
print(wrong)
return
I wrote a compiler for this DSL, which was then used to compile the algorithm into an OISC program executable by the OISC VM. The OISC program is then packed together with the OISC VM as a standalone binary, which is delievered to the players.
Multiple Solutions - Behind the Scenes
During the competition, I was surprised to notice that multiple solutions exist. A quick debugging revealed the cause: the implementation of outofnumbers (var) in the compiler was incorrectly written in a way similar to return var not in range [0...9]. Since the Sudoku map is supposed to only contain 1 ~ 9, the correct implementation should be return var not in range [1...9]. Under such a scenario, multiple solutions exist because we allow the grids to be filled with 0.
Sudoku Map
Solution
To solve this challenge, there is no need to simplify all the logical operations. Since there is no complicated loop in the actual control flow, we can locate the conditions preventing the control flow from jumping to the part which outputs “Sorry” through simple control flow tracing and (manual/automated) symbolic analysis. Along the way, we extract the constraints for the non-Sorry branches. Finally, we can use an SMT solver to solve the constraints. (That’s how ThinerDAS solved this challenge.)
Flag: d3ctf{g5lk9t28zz47y3l6m2kosbajd2vk9e2dwghxgfktcki}
The source code of this challenge (except for the compiler) and a duplicate of this post are uploaded to GitHub, check them out at: https://github.com/yype/D3CTF_Rev/tree/master/AncientGameV2.
More..
I’ve always found OISC interesting. This challenge is just a demo of one of my ideas. I’m considering doing more interesting works related to OISC in the upcoming future.